By observing the smaller animated #gif on your right, you may fall under the impression that all of the dots rotate together, simultaneously forming a spinning circle as they move along. But look what happens when we map their trajectories, and make their paths visible!
As you can see, (as can be seen from the animated solution below )- it turns out each dot moves independently, up and down along a straight line. I presume the toughest part (for the unknown author) was to get them all synched-up, forming a perfect circle as they move. It’s a really nice optical illusion, one that greatly reminds me of our recent “Circling Flower“. What do you think? Is it effective?
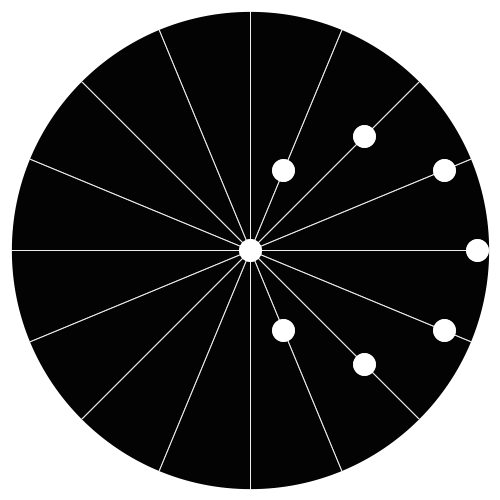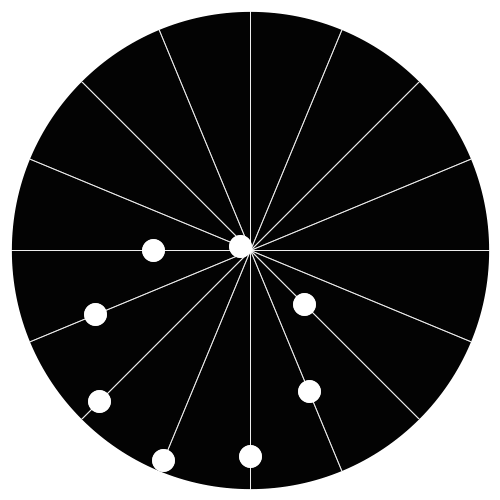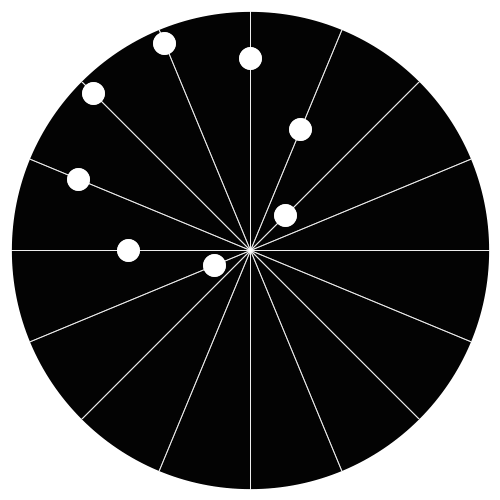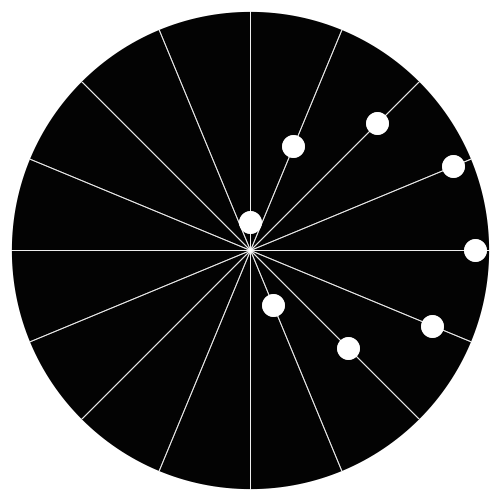
Amazing, very nice!
It shouldn’t have been difficult for the author to get the dots lined up. I believe that as long as the small circle has half the radius of the large circle, then any dot, placed anywhere on the edge of the small circle (the dots don’t have to be evenly spaced or anything) will move along a straight line in this manner when the smaller circle “rolls” around the larger one.
COOL! :D
It’s called mathematics! Arrange any set of points on a circle like this and rotate the circle at a fixed distance from a point equal to its radius. Voila!
Actually, the dots do rotate together. And they do oscillate across the larger circle in straight lines.
It depends on whether you’re using a normal frame of reference, or a rotational frame of reference. The curiosity is the mind preferring to observe the rotational frame of reference.
It’s a Hypocycloid. Like Spirograph.
That’s pretty cool. But is it really an optical illusion? I guess by that I mean do the white dots remain fixed relative to each other each other so that if you stopped it at any point in time you could draw a perfect circle connecting the dots? That’s certainly how it appears, but are you saying that’s actually an illusion and they don’t really remain fixed points on a moving circle? Or they do and this is more a geometric marvel and not really an illusion?
Part of the effect comes from the fact that the dots slow down when they reach the outside of the large circle, which can be seen clearer on the diagram with lines on it.
What if we apply 4 dimension theory to this, such as hypercubes?