Just came back from Paris yesterday evening. Can’t say I enjoyed much. Apart from marvelous architecture and breath-taking historic sights and museums, it felt like any other European metropolis. Perhaps I expected too much, thus was little bit disappointed. I enjoyed seeing Napoleon’s resting place at Les Invalides, and Louvre museum the most. There were so much tourists, I couldn’t stop feeling like one. Perhaps if I had some local friends, they could help me experience local life (and point me where I could eat some good food), ultimately making the trip much more interesting…
Sorry for such a long intro, just wanted to inform you I’m back now (and how last few posts were set to automatically appear each day, and were written few days ago ;). It’s also why it took so much time to get your comments approved. Now that I have charged my batteries once again, let me roll up my sleeves and continue sharing some good stuff! For today I bring you two posters that feature Missing Pieces illusion we featured some time ago. Seems that Chupa-Chups company jumped the optical illusion billboard wagon as well!
http://en.wikipedia.org/wiki/Paris_syndrome
Something like that?
How on earth..?
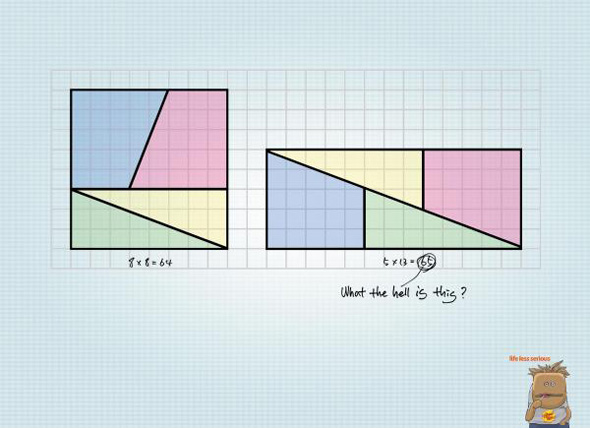
Just note if the lines were not so thick, one might notice that the points (0,0), (5,2)-the top of green triangle on lower figure, and (13,5)-top of the pink triangle do not lie on a straight line and so the pieces are not actually the same dimensions. nice image in that one can hide an entire 1X1 square in the edges… daa
Whats your IQ?
the hole is explained: http://www.marktaw.com/blog/TheTriangleProblem.html
the 64=65 one is similar. they just don’t line up.
I can’t work this one out. It’s like the bottom one is smaller by a tiny bit because I’ve counted the blocks and lines and they’re both the same. Thats for the second one.
As for the first one isn’t it just a stupid math error?
Nah. It isn’t a calculation mistake. the reason behind the different area is due to the arrangement of the figures. the exact mathematical reason, I am not so sure. But I am sure it works, I saw it before somewhere.
My brain just refuses to deal with this!
http://www.youtube.com/watch?v=ee0dksxkog0 and many other sites explain this illusion.
Also, I love Paris in the the springtime :-)
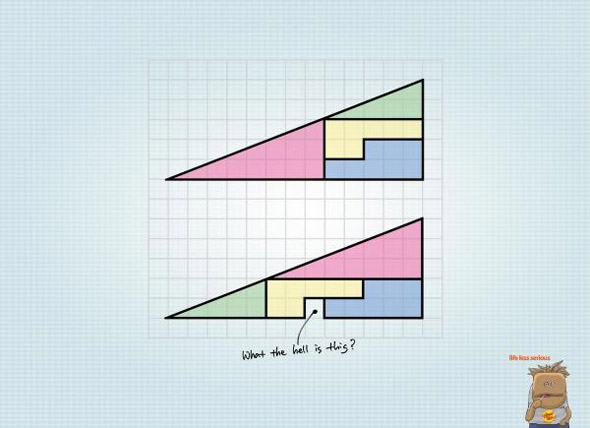
The pieces from the first puzzle do not fit together tightly in the second puzzle. In reality there should be a skinny gap along the diagonal to account for the extra square. The heavy black line covers this gap.
Calculate the slopes of the diagonal edges of each piece and you will see they are not the same.
Attached is a more precise version of “Chupa-Chups Missing Pieces” to show how it is done.
The pieces from the first puzzle do not fit together tightly in the second puzzle. In reality there is a skinny gap along the diagonal to account for the extra square. The heavy black line covers this gap.
Calculate the slopes of the diagonal edges of each piece and you will see they are not the same.
[img]http://img545.imageshack.us/img545/2081/chupachupsmissingpieces.jpg[/img]
Beautiful. Great example.
Does anyone know how to send in illusions…? Because I found a pretty good one (form another illusion) and I don’t know how to send it in.
How to send illutions: right by the ‘submit comment’ button, there is a little note saying, “you can add some images too.” click on the blue and your there. i dont know how else do do it b/c i havent clicked it. so reply if this helped!………;)
That is helpful, but it isn’t strictly to do with this illusion. More of it’s own separate thing. I wanted to send it to Vurdlak because I’, not sure if he checks all the comments. Thanks, though!
Folks. This month’s (May-June 2011)edition of Scientific American has an entire section dedicaled to Illusions along with links and some DIY articles.
Haha I’m too analytical and mathematical to enjy these. They just really bug me :) even when knowing how it’s done…
Sorry Folks, That’s Scientific American MIND…
okay what what and yes i will say it again what
they both work on the illusion of the shapes not being entirely what they represent.
for instance, the triangle example is not actually a triangle but a f sided shape, for it ti be a true triangle the three triangle elements (pink green and whole) need to be similar, and if this were true then
pink height/pink width == green height/green width == whole height/whole width
pink height/pink width = 3/8 = 0.375
green height/green width = 2/5 = 0.4
whole height/whole width = 5/13 = 0.385
because these ratios are different we can see that the triangles are not similar, proving that the whole shape is not a true triangle
All I have to say is… What the hell!!!!
Ah yes the old chessboard paradox. Visaully striking, Fibernachie number serices issues. But simpy the diabonal angle of the 4 sided pieces is just not the same as the diagonal angle of the the three sided pieces. So the apparently stright line ( or diagonal) through the long rectangle is simply not one line, there is a “void” in the middle and it accounts for the “extra” block or apparent extra block.
brooks
One of the only examples where the algebra I skill of finding slopes is useful in the world of optical illusions.
Different shapes can make different shapes. Lol.
Reading Danny Dulai’s suggestion, that makes sense!
Draw it in a cadd program and it’s perfectly clear. They aren’t the same size. The difference is subtle but distinct when dimensioned. It’s just like an architect’s drawing: If it doesn’t quite fit, use a different line weight. They’ll figure it out in the field.
this is sameeeeeee
The first figure works cause of the arrangement of the figures. If you were to arrange them in real, you will discover a small spacing, a quadrileteral with area = 1cm(2). Hence, it will have a different area. It is not a calculation error!
The second one is basically the arrangement of the figure that causes the hole. Danny Dulai(third commentor of this post) has a link to the full explanation.
I remember this from school, though the working example was different – an 8 x 8 slab of cake, that needed to feed 65 people. By chopping and arranging like that, before chopping again, you’d actually get a reasonably fair distribution of cake.
Reasonably….
Welcome home, sorry you didn’t enjoy it; I told you to hit the wine! As for this illusion it goes right over my hear, WHOOSH!!………:)
i feel like i dont have a brain when i look at that! who else thinks so?!
The cosines of the smaller angles of the two tringles are not equal. hence the smaller angles of the two triagles are not equal.This proves that the line opposite the right angle of the combined figure is not a straight line.
yes in the first puzzle ideed it is 13×5=65. no other way to look at it.
The Slopes of The two Lines are Different.Human eye unable to see that difference
impossible!!!
Nothing got lost. It is still the same size surface…
that space is normal because the non triangular pieces were forced to collapse by the difference in size of the triangles that were interchanged…. so lets not be fooled by the “empty” space. one triangle was three grids high and the other was two….I think this illusion can only be achieved with these exactly sized elements.(it’s not because its not colored that its not there)
You guys are argue too much!
This is the solution for this problem:
[img]http://upload.wikimedia.org/wikipedia/commons/1/1a/Missing_square_puzzle_animation.gif[/img]
Guys guys guys, the 2nd one is so freaking easy, on the top part, notice how the yellow brick was places ON the blue brick.
By on the one below, the yellow was places BESIDE the blue brick.
But why do they both have the same length?
Because the green and red brick changed sides.
This is easy if you think of you secondray school mathamatics. The difference is because you’re not comparing two alike shapes. Rectangles have a fairly crear exponencal area increase is X x Y. While the triangles have to comply to pythagoras’ theorem where the sides and area increases work in a different way. ie c is equal to the root of a sq + b sq. as such the triangles can manstain the same angeled increase but reqult with a different side lengths while the increase of the rectangle increases like i said before X x Y. this optical trick just uses some clear cuts in the shapes to point that out. (o.o)
Here’s a hint: 2/5≠3/8